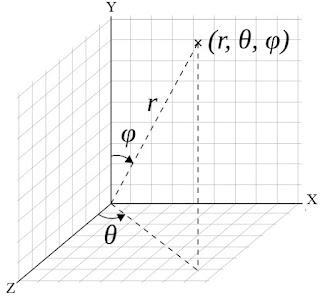
Spherical Coordinates

-


A spherical coordinate system is a coordinate system where the position of a point in 3D space is specified by three numbers:
  • a radial distance r
  • an azimuthal angle θ (theta)
  • a polar angle φ (phi)
Spherical coordinates comes in handy to implement an Arcball Camera.

Imagine to have a virtual ball behind your screen, by clicking with your mouse you pinch the ball and by dragging the mouse you make the ball spin around its center.

We can map the mouse x coordinates to be the θ angle and the mouse y coordinates to be the φ angle.
We also assume that our virtual ball is a unit sphere so the radial distance is always 1.
The problem is that we can specify the position of our camera only using cartesian coordinates so how do we convert spherical coordinates to cartesian coordinates?

Polar Coordinates

Polar coordinates are like spherical coordinates but in 2D. 


We can specify the position of a point using two numbers:
  • a radial distance r
  • an angle
We use polar coordinates to break down the conversion from spherical to cartesian coordinates in two 2D problems.
First we'll compute the position of a point P on the XZ plane using angle θ, then we compute the position of a point P' on the XY plane using angle φ.

Convert spherical coordinates to cartesian coordinates

Computing the position of point P from polar to cartesian coordinates is simple:

Xtheta = cos(θ)
Ytheta = sin(θ)

and here's how we compute the position of point P':

Xphi = cos(φ)
Yphi = sin(φ)

Now how these two points are related?
Look at the following picture:


The circle of angle θ through point P becomes smaller the higher (or lower) it sits in the unit sphere.
P' controls how high or low it sits in the unit sphere.
So in other words we can say that Yphi controls how high or low circle theta sits in the unit sphere while Xphi controls how large its radius is going to be.

Let's say X, Y, Z are the final cartesian coordinates, we compute the position of our camera as follows:

X = Xtheta Xphi r
Y = Yphi r
Z = Ytheta Xphi r

We add r to the equations just in case the radial distance is > 1 or < 1.
Using cos and sin functions the final formula becomes:

X = cos(θ) cos(φ) r
Y = sin(φ) r
Z = sin(θ) cos(φ) r

Comments

Post a Comment

Popular posts from this blog

GLSL Shader in Maya Part 1

-
Image
Maya to act like an (expensive) shader editor There aren't many shader editors out there, not as many as it used to be in the early 2000s when AMD had RenderMonkey and Nvidia had FX Composer. They were pretty good softwares in my own humble opinion and it's a pity they have been discontinued. These days we have Shadertoy but to be honest I prefer native applications, yes I'm old school! I've always known that Maya supports HLSL and GLSL shaders in Viewport 2.0 so I've started to think that it would be really cool to use it like a shader editor. But it's not as simple as I would have expected, the documentation around the net is pretty sparse so it's a matter of trials and errors. Why GLSL and not HLSL? I have nothing against HLSL, in fact I use it extensively in Unity (well to be precise I use Cg which is NVidia version of HLSL). I've decided to go with GLSL simply because is more portable and I like to use Maya on Linux for my person...
Read more

Unity Shader: Toon Water Shader

-
Image
  I'm a huge fan of Studio Ghibli movies and I've always wanted to replicate their visual style in a video game. In this post I'll tell you how I emulate as close as possible, the look of the water we all love in Studio Ghibli movies. Before we continue, I'd like to thank Roystan and Harry Alisavakis for their tutorials on toon water  and grab pass shaders which gave me the kickstart to develop my own water shader. Features I wanted my shader to be quick and easy to insert in a scene, so all you need is just a flat plane that will be our water surface and some kind of terrain with depth to contain our water. The shader will have the following features: animated vertex displacement animated fake refraction selective planar reflection animated normal maps animated foam How it works We can subdivide the shader into 5 steps: Vertex displacement - use a simple vertex displacement map to generate waves moving the vertices of the flat plane along the y-axis. Depth based w...
Read more

Unity Shader: Spherical Mask Dissolve

-
Image
Spherical Mask Dissolve Shader This shader is the combination of the two previous shader, the Dissolve shader and the Spherical Mask shader to get a "reveal world" kind of shader, something like you have experienced in games like Beyond Eyes . If you remember, in the Dissolve shader we used a  _DissolveTexture  to get a dissolve_value . Because the dissolve_value is in the range of (0,1) we needed an _Amount value to be subtracted from the dissolve_value so that the clip() function can discard all the pixels that has a dissolve_value < 0. In the Spherical Mask Dissolve shader we don't have an _Amount value, instead we have to compute it! To compute the _Amount value (that in this shader is called amount) , we use the technique showed in the Spherical Mask Shader. In the Spherical Mask Shader we checked if a pixel was inside of the player radius of action, if it was we color it, if it wasn't we let it in grayscale. Here we use the same logic to define ...
Read more